树的定义本身就是递归的，因此树的基本操作用递归是很容易实现，代码也很美观，下面总结了二叉树的三种遍历方式，并用Golang进行了实现。

定义

二叉树的遍历就是按照某条搜索路径访问二叉树的每一个节点，且每个节点只访问一次。

图1 二叉树
如图1所示，如果限制先左后右遍历，则有三种遍历方案，按照根的访问顺序不同，有：
  • DLR：前序遍历
  • LDR：中序遍历
  • LRD：后序遍历

算法

图2 二叉树用例

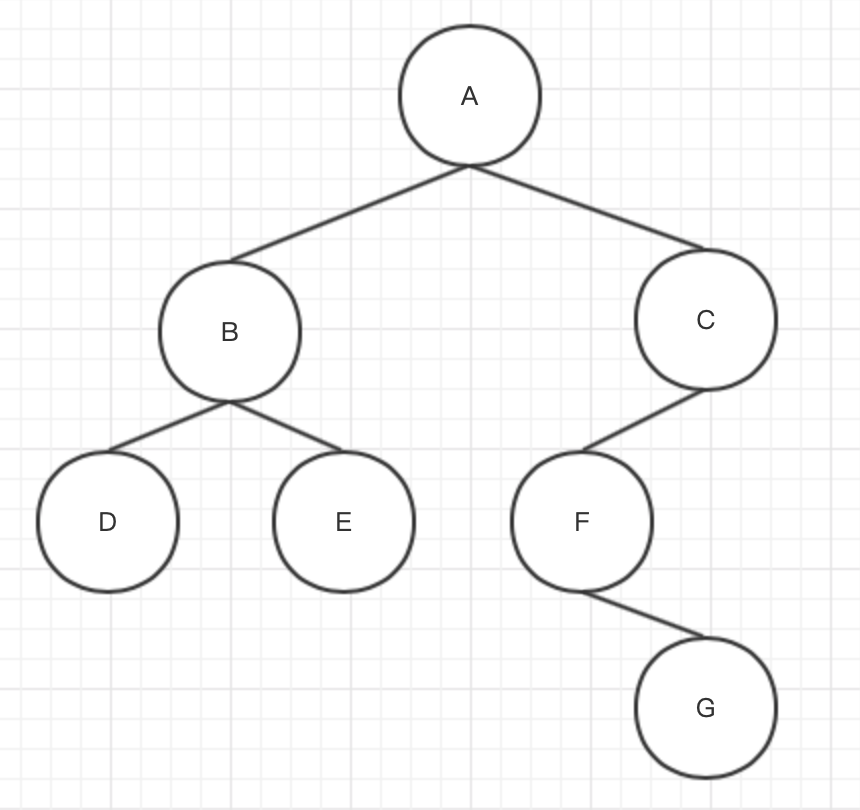
节点定义统一为：

type Node struct {
	value string
	left  *Node
	right *Node
}

前序遍历

访问根，然后遍历左子树，左子树为空或已遍历才可以遍历右子树。

结合图2所示

  1. 先访问根结点A，然后访问A的左子树BDE；
  2. 对于左子树BCD而言，先访问根B，然后再访问左子树D；
  3. 遍历D的左子树，发现为空，于是返回，遍历D的右子树，也为空，于是返回到B；
  4. 访问B的右子树E，同理，E的左右子树都为空，返回到最初的根结点A，开始访问A的右子树；
  5. 访问节点C，再访问C的左子树，节点为F；
  6. 再访问F的左右子树，结果为G，然后返回到C；
  7. 访问C的右子树，发现为空，至此，遍历结束。

最后的结果为：ABDECFG
用递归的写法为：

func preOrder(root *Node)  {
	if root == nil {
		return
	}
	fmt.Println(root.value)
	preOrder(root.left)
	preOrder(root.right)
}

中序遍历

中序遍历左子树，左子树为空或已遍历才可以访问根，中序遍历右子树

结合图2所示

  1. 中序遍历A的左子树BDE，对于BDE来说，再遍历B的左子树D，D的左右子树为空，所以返回D；
  2. 访问B，接着访问B的右子树E，E的左右子树都为空，则返回E；
  3. 至此，A的左子树访问完毕，则访问根结点A，接着访问A的右子树CFG；
  4. 先访问C的左子树F，F的左子树为空，则访问根结点F，再访问F的右子树G；
  5. G的左右子树都为空，则返回G；
  6. C的左子树遍历完毕，返回C，再访问C的右子树，为空，则遍历结束。

最后返回结果为：DBEAFGC
用递归实现为：

func inOrder(root *Node)  {
	if root == nil{
		return
	}
	inOrder(root.left)
	fmt.Println(root.value)
	inOrder(root.right)
}

###后序遍历

后序遍历左子树，后序遍历右子树，左右子树为空或已遍历才可以访问根

结合图2所示

  1. 先遍历A的左子树BDE，对于BDE而言先遍历B的左子树D；
  2. D的左右子树为空，返回D，再遍历B的右子树E；
  3. E的左右子树为空，返回E，再访问根结点B，至此，BDE遍历结束；
  4. 再遍历A的右子树；
  5. 先遍历C的左子树，F的左子树为空，则遍历F的右子树G，G的左右子树为空，则返回G；
  6. 再访问F，接着遍历C的右子树，为空，于是访问C；
  7. 最后访问根结点A，至此，遍历结束。

最后返回结果为：DEBGFCA
用递归实现为：

func posOrder(root *Node)  {
	if root == nil{
		return
	}
	posOrder(root.left)
	posOrder(root.right)
	fmt.Println(root.value)
}